Last updated: 2026-02-22
Homework instructions/advice:
Define A and b as follows: A = \begin{bmatrix} 3 & 7 & 6 \\ 4 & 1 & 4 \\ 3 & 8 & 7 \end{bmatrix}, b = \begin{bmatrix} 2 \\ 4 \\ 6 \end{bmatrix}
Solve the matrix-vector equation Ax = b using row-reduction. You should get integer results.
Define A as follows: A = \begin{bmatrix} 1 & 4 & 1 \\ 7 & 5 & 7 \\ 8 & 4 & 8 \end{bmatrix}
Show that A is not invertible, and give a nontrivial solution to Ax = 0.
Define A as follows: A = \begin{bmatrix} 1 & 4 \\ 7 & 5 \end{bmatrix}
Find AA^\intercal.
Give a counterexample that shows matrix multiplication is not commutative for 2\times 2 matrices.
Show that I_2A = A for all matrices A with dimension 2\times 2.
A small bakery makes two types of muffins: blueberry and chocolate chip. Each blueberry muffin requires 0.5 cups of flour and 0.25 cups of sugar. Each chocolate chip muffin requires 0.5 cups of flour and 0.5 cups of sugar. The bakery has 20 cups of flour and 15 cups of sugar available each day. The profit from each blueberry muffin is $2, and the profit from each chocolate chip muffin is $3. The bakery wants to maximize its daily profit.
You will create and solve a linear program that models the above scenario:
Note: this problem is a little more complex than the above problem, but is still possible to model using 3 decision variables (for the obvious quantities).
A furniture company produces three types of chairs: basic, deluxe, and executive. The production of each chair requires different amounts of wood, labor, and fabric. The company wants to maximize its profit given its limited daily resources.
The company’s goal is to maximize profit. The profit for each chair type, along with its material cost, is as follows:
The company has these additional constraints:
You will create (but not solve) a linear program that models the above problem:
Give an example for each of the following types of linear programs:
In class, we saw that the intersection of convex sets was convex. Is the union of convex sets convex? If so, explain. If not, provide a counterexample.
Determine the big-O time complexity of the function f in the below piece of code, in terms of the length of the array A.
def f(A, target):
# A is a sorted list of integers
lo = 0
hi = len(A) - 1
while lo <= hi:
mid = (hi + lo) // 2
m = A[mid]
if m == target:
return mid
elif m < target:
lo = mid + 1
else:
hi = mid - 1
return -1 Determine the big-O time complexity of the function g in the below piece of code, in terms of n.
def g(n):
x = 0
i = 0
j = 1
while i < n:
x += 1
i += j
j += 1
return xState the time complexities for each of the following operations, in big-O notation. (Disregard amortized vs. non-amortized time.)
What does it mean for something to run in polynomial time? Why is it important?
Evaluate this expression:
\sum x \quad \forall x, 0\leq x\leq 100, x\equiv 0 \bmod 6
Evaluate this expression:
\prod_{i=1}^5 i^2
Formalize as a linear constraint each of the following statements, given a graph G = (V,E) and cost function C: E\to \mathbb N.
Use the “\forall” and “\sum” notation we covered in class, and use a decision variable x_{i,j} to denote the flow from vertex i to vertex j.
Note that C is cost, not capacity. To determine the cost of an edge (i,j)\in E in an LP solution, you must multiply the cost of the edge C((i,j)) by the amount of flow through (i,j), given by x_{i,j}.
Constraints to model:
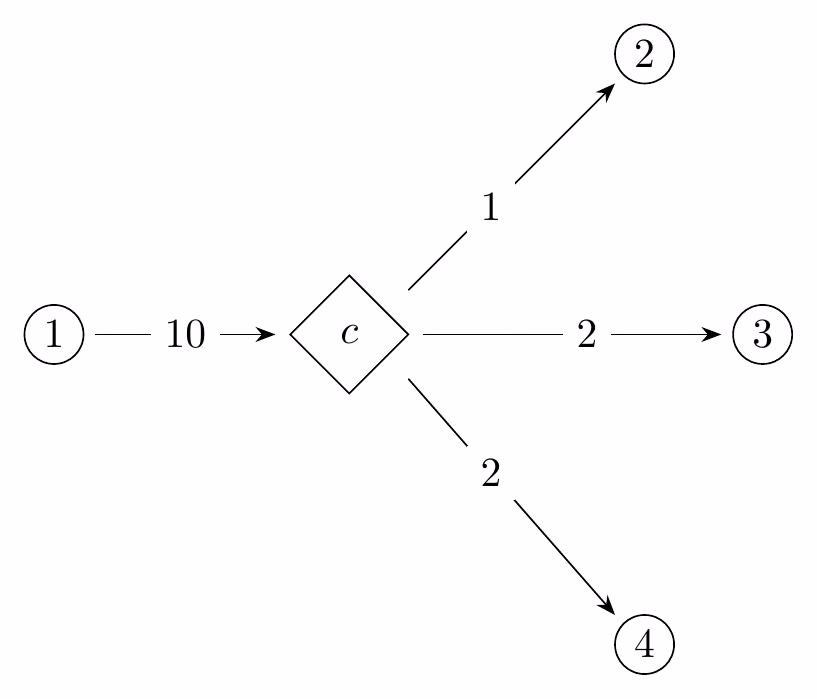
Suppose you are given a graph G = (V,E) and vertices s,t\in V, and you are asked to model the maximum flow problem for G. However, you are also given a new type of vertex called a combiner, which requires two units of input flow for each unit of output flow, as seen in the below examples. A combiner can have any number of inputs or outputs, but the totals have to have a 2:1 ratio.

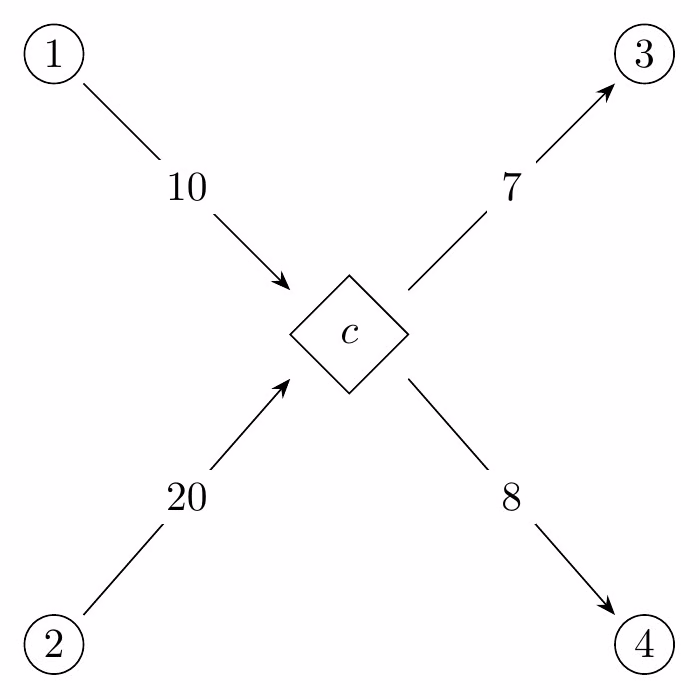
Combiners are also vertices, in the set C\subset V.
LP Model: Describe how you will model max flow on G as an LP with this modification:
Integrality: In class, we saw that for max flow, if all capacities were integer then all flows would be integer in the solution to the LP. Does that hold for this formulation? If so, explain why. If not, provide a counterexample.
For each of the following constraints on the decision variable x, state whether they can or cannot be modeled by a linear program:
For each of the following constraints on the decision variable x, state whether they can or cannot be modeled by a linear program:
END OF HW 1