Last updated: 2025-03-07
This assignment is due March 22nd at 11:59 PM. Submit your solution on BrightSpace, under the “Unit 7” assignment.
Please copy your code into the text box, making sure to indent it properly with whitespace so that it appears the same as in IDLE or wherever you wrote the code. This will make it easier for me to grade.
You can submit multiple times. I will only grade your last submission.
This assignment uses a text file poly.txt, which you can open by clicking here: poly.txt

A cubic polynomial is a function of x of the form Ax3 + Bx^2 + Cx + D, where parameters A, B, C, and D are real numbers. Consider three concrete examples: \begin{gathered} P_1(x) = x^3 - x^2 + 4x - 30 \\ P_2(x) = x^3 + 0.5 x^2 + x - 6 \\ P_3(x) = 3x^3 + 13.6x^2 + 13.2x + 37.8 \end{gathered}
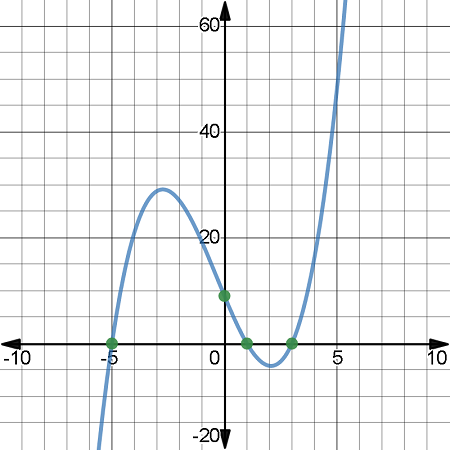
A root of a cubic polynomial P(x) is a value r such that P(r) = 0. The intuitive description of a root r is that P(x) hits the x-axis at x = r. There may be multiple roots, because P(x) may pass through (or touch) the x-axis multiple times (see the provided graph of a cubic polynomial).
For example, r = 3 is a root of P_1 as defined above, because P_1(3) = 3^3 - 3^3 + 4 \cdot 3 - 30 = 27 - 9 + 12 - 30 = 0:
In Python, a polynomial can be implemented as a function. The three examples above can be written as follows:
def P1(x):
return x*x*x - x*x + 4*x - 30
def P2(x):
return x*x*x + 0.5*x*x + x - 6
def P3(x):
return 3*x*x*x + 13.6*x*x + 13.2*x + 37.8Note: Roots of polynomials can be found using the function
goalSeek(discussed in class), if you supply the tested polynomial function as thefunctionparameter, set the target parameter equal to zero, and start with a goodlowLimitandhighLimitinterval enclosing the root.More important note: The function
goalSeekrequires that the tested functionfhave the property thatf(lowLimit)\leqf(target)\leqf(highLimit). (We saw that there was an issue withgoalSeekon question #4 in class when this condition did not hold.) All polynomials provided for this task will satisfy this requirement.
For this task, you are provided with the file poly.txt containing coefficients of 25 polynomials. The first few lines of the file look like this:
# A B C D Lo Hi Formula
3 -1.8 -7.6 -20.8 -4.28 11.88 3 x^3 - 1.8 x^2 - 7.6 x - 20.8
2 5 14 24 -6.57 0.73 2 x^3 + 5 x^2 + 14 x + 24
2.7 7.59 9.49 3.85 -1.86 5.85 2.7 x^3 + 7.59 x^2 + 9.49 x + 3.85
1 0 -8 -32 0.44 10.58 x^3 - 8 x - 32The first line is a header, which you will have to skip when reading the file. (You can just check whether the line has a # at the start.) Each of the following lines starts with four coefficients A, B, C, and D, uniquely determining a polynomial Ax^3 + Bx^2 + Cx + D.
The coefficients are followed by the suggested values for the limits Lo and Hi on the search range. Each provided polynomial is guaranteed to have exactly one root in the interval Lo \leq x \leq Hi. We will use goalSeek to find this root for each of the provided polynomials.
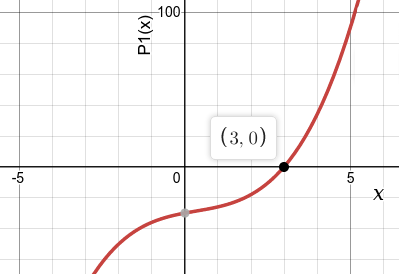
The last column of the file contains a conventional representation of the polynomial, which you can paste into WolframAlpha to confirm that your program correctly finds the roots. For example, here is the response for the first polynomial in the file, which says that the real root is equal to 2.6.
In this task, we are going to write a program that finds the roots of cubic polynomials listed in the file poly.txt using goalSeek function.
goalSeek function to find the roots of the polynomials P_1, P_2, and P_3 listed in the introduction. The expected answers are 3, 1.5, and -4.2 respectively. Choose the limits to contain the roots you are looking for (-5 and 5 would suffice for these three polynomials). Confirm that your program is finding correct roots.poly.txt. Discard any line that starts with a # symbol (thus skipping the header). For each non-header line, split it and use the function float to extract A, B, C, D, Lo, and Hi. Print them out to confirm that your program correctly extracts these numbers.
!= to check that two values are not equal. For example, the condition line[0] != '#' evaluates to True if the first character in line is not equal to #.makePoly that can generate a Python function representation of a cubic polynomial from its coefficients A, B, C, and D. For example, the polynomial function P_1 we used earlier could be created with the generator function as seen below:# original function P1
def P1(x):
return x*x*x - x*x + 4*x - 30
# function P1 created using the makePoly function
P1 = makePoly(1, -1, 4, -30)makePoly to generate its Python function representation.
goalSeek on this function with given Lo and Hi limits to find the root. You can use WolframAlpha to check that the roots are correct.-> to clearly separate the root from the coefficients): 3.00 -1.80 -7.60 -20.80 -> 2.60
2.00 5.00 14.00 24.00 -> -2.00
2.70 7.59 9.49 3.85 -> -0.70
1.00 0.00 -8.00 -32.00 -> 4.00
1.80 -9.94 -29.38 -20.28 -> 7.80
1.00 13.40 24.80 22.80 -> -11.40
2.10 -18.64 -8.44 -17.86 -> 9.40
1.00 19.20 46.45 31.35 -> -16.50
3.00 -23.60 -1.20 -57.40 -> 8.20
3.00 -54.70 -87.50 -238.80 -> 19.90
2.50 -16.30 -31.24 -26.24 -> 8.20
0.70 12.78 10.74 5.22 -> -17.40
3.00 -15.90 -16.90 -12.60 -> 6.30
0.90 6.46 17.64 48.60 -> -5.40
0.90 -0.18 -25.18 -51.46 -> 6.20
2.00 -5.00 7.00 -30.00 -> 3.00
2.40 -13.12 -10.76 -74.80 -> 6.80
2.00 18.20 23.20 56.70 -> -8.10
2.80 41.86 71.38 88.44 -> -13.20
2.00 6.20 11.00 4.80 -> -0.60
0.80 -2.46 2.96 -61.36 -> 5.20
1.00 10.00 32.00 77.00 -> -7.00
1.00 -4.00 -3.00 -10.00 -> 5.00
2.00 3.80 7.60 -0.80 -> 0.10
2.00 5.60 6.90 3.90 -> -1.30maxError.You should be able to do all of the tasks with only the Python topics we covered in class so far.
If you want to use more complex functionality than what we discussed in class, the Python documentation may be helpful: Python 3.10 documentation