experiments with integer sequences, mod, and knight moves

I recently watched a YouTube video by Jacob Yatsko on using the Fibonacci numbers modulo various constants to create cool patterns. In the second half of the video, he talks about something he calls "Pisano left-right graphs", which basically take the Fibonacci numbers mod some constant and then based on parity either move left or right. These graphs tend to exhibit some interesting symmetry as a result of the underlying sequence's period when taken mod a given constant, which for Fibonacci numbers specifically is called the Pisano period.

I thought this was really cool and knew that I could expand on the idea with some quick matplotlib work.

This post contains some of the experiment results I thought were interesting.

The experiment

In the video, the left and right movements were purely along the gridlines: left meant a 90 degree rotation left, and right meant a 90 degree rotation to the right.

For my experiment I decided to take it one step further, and use knight (as in chess) moves. The logic for left/right movement turned out to be a bit more difficult but after drawing it out it wasn't that bad.

As in the video, I chose an arbitrary direction to start of $(1,2)$. From there, I used a sequence to determine whether to go left or right, first taking the number mod some constant, and then going left if the result was even and right if it was odd.

For example, for the Fibonacci numbers mod 3:

• 1 is 1 mod 3, so the result is odd. Go right.
• 2 is 2 mod 3, so the result is even. Go left.
• 3 is 0 mod 3, so the result is even. Go left.
• 5 is 2 mod 3, so the result is even. Go left.
• 8 is 2 mod 3, so the result is even. Go left.
• 13 is 1 mod 3, so the result is odd. Go right.

...and so on.

One thing to note about these results is that for certain mod constants, the results are pretty boring. Specifically, for any even mod constant, you get something like the following (this time, using the squares):

• 1 is 1 mod 4, which is odd, so go left
• 2 is 2 mod 4, which is even, so go right
• 3 is 3 mod 4, which is odd, so go left
• 4 is 0 mod 4, which is even, so go right
• 5 is 1 mod 4, which is odd, so go left
• 6 is 2 mod 4, which is even, so go right
• 7 is 3 mod 4, which is odd, so go left
• 8 is 0 mod 4, which is even, so go right

...and so on. The effect of even mod constants will be clearly visible in some of the visualizations that follow.

Because of this simplifying effect, for the most part I only included the results of odd mod constants in the visualizations.

For the purpose of visualizing the progression of the walks, I used the 'cool' matplotlib color map, which made the color of each segment vary from cyan to magenta.

Also, I set the number of steps to 10000, which was more than enough to accomodate most of the periods (as seen later).

Fibonacci numbers

I started with the Fibonacci numbers in the same way as the original video:

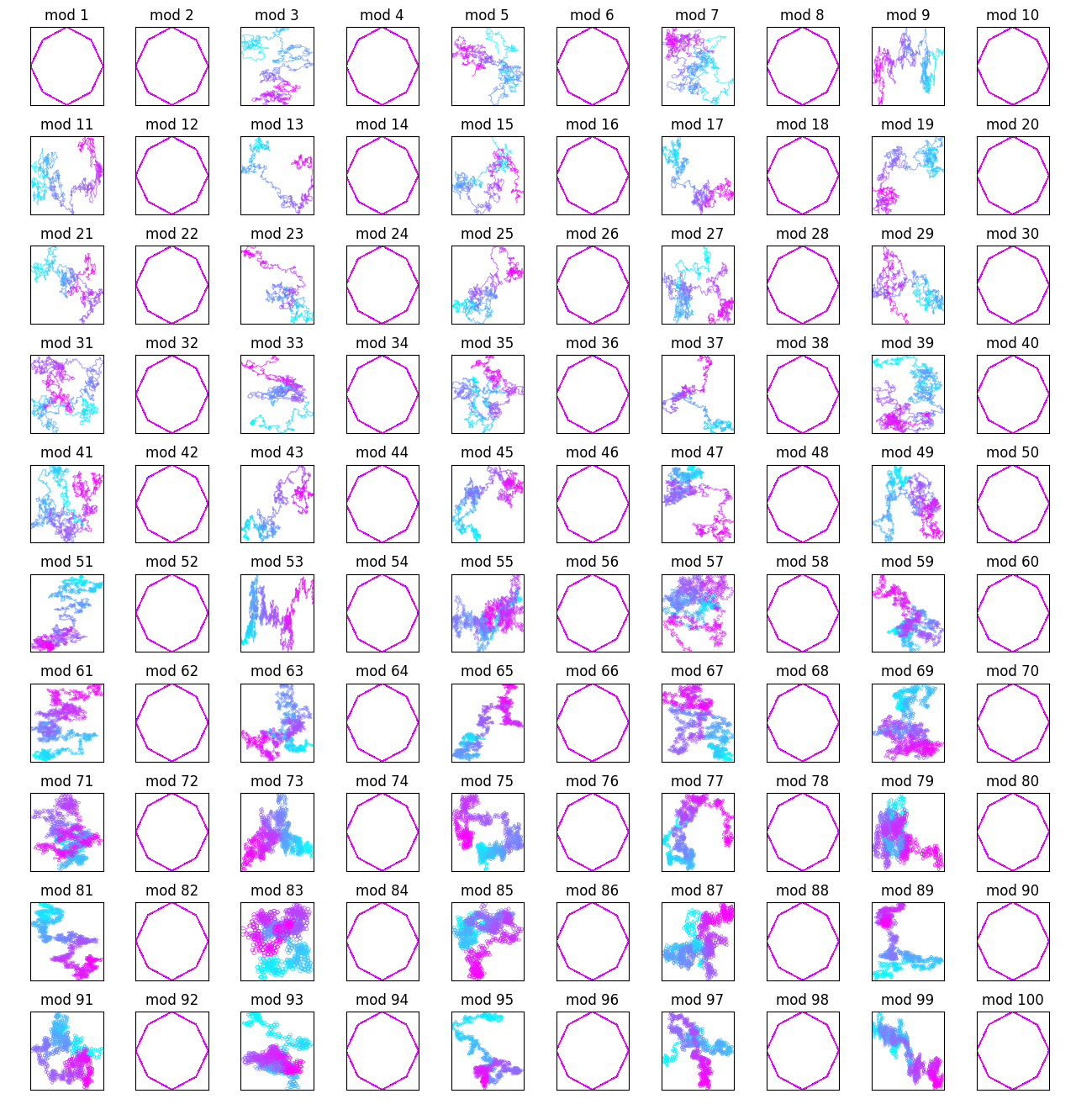
Noticing the similarities of the even mod constants, I excluded them and went up to 200:

There are some pretty cool patterns here. Most of them seem to be spirals, or otherwise have some sort of symmetry (I guess this would be related to the Pisano period somehow). Some, however, are more linear, going off into space in one direction or another.

As mentioned above, the number of steps used was 10000, which was enough to cover most periods many times over. It's possible to see this because most of the symmetric (visually periodic) structures generated are all colored purple, meaning that they were traced over towards the end of the color spectrum.

Lucas numbers

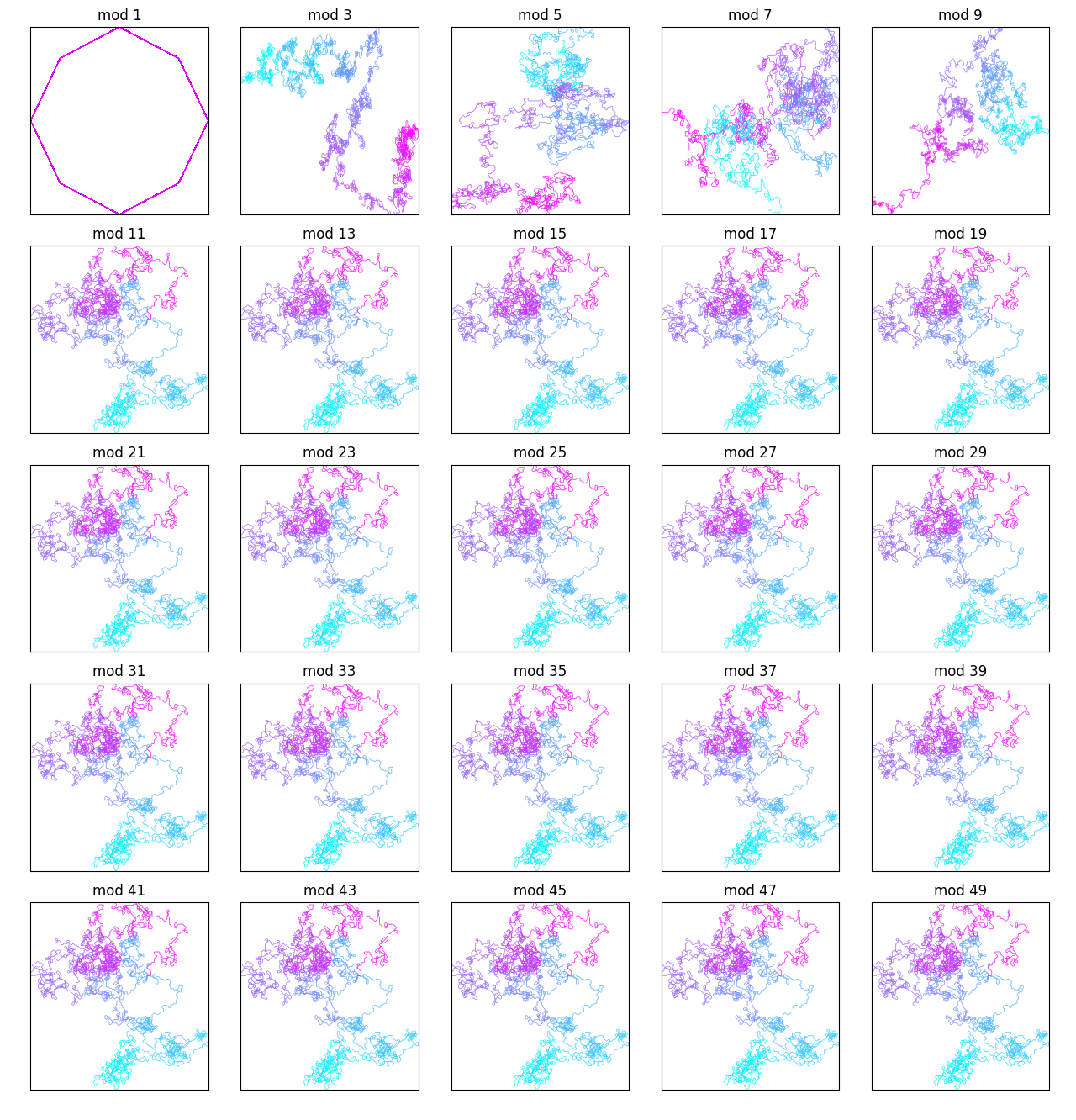
The next numbers to try were of course the Lucas numbers, which are the cousins of the Fibonacci numbers (starting with $(2, 1)$ rather than $(1,1)$):

There were some similarities here: lots of spirals. But for these numbers there seemed to be many more straight lines (visually aperiodic structures).

Squares, cubes, and other powers

Next I tried looking at the natural numbers raised to various powers:

Definitely some interesting designs here. It looks like even powers exhibit radial symmetry, while odd powers only exhibit rotational symmetry.

What about the power of 1? Well, it's not too interesting:

Also, as discussed before here are the squares including evens:

Yeah, the evens aren't super interesting here.

Primes

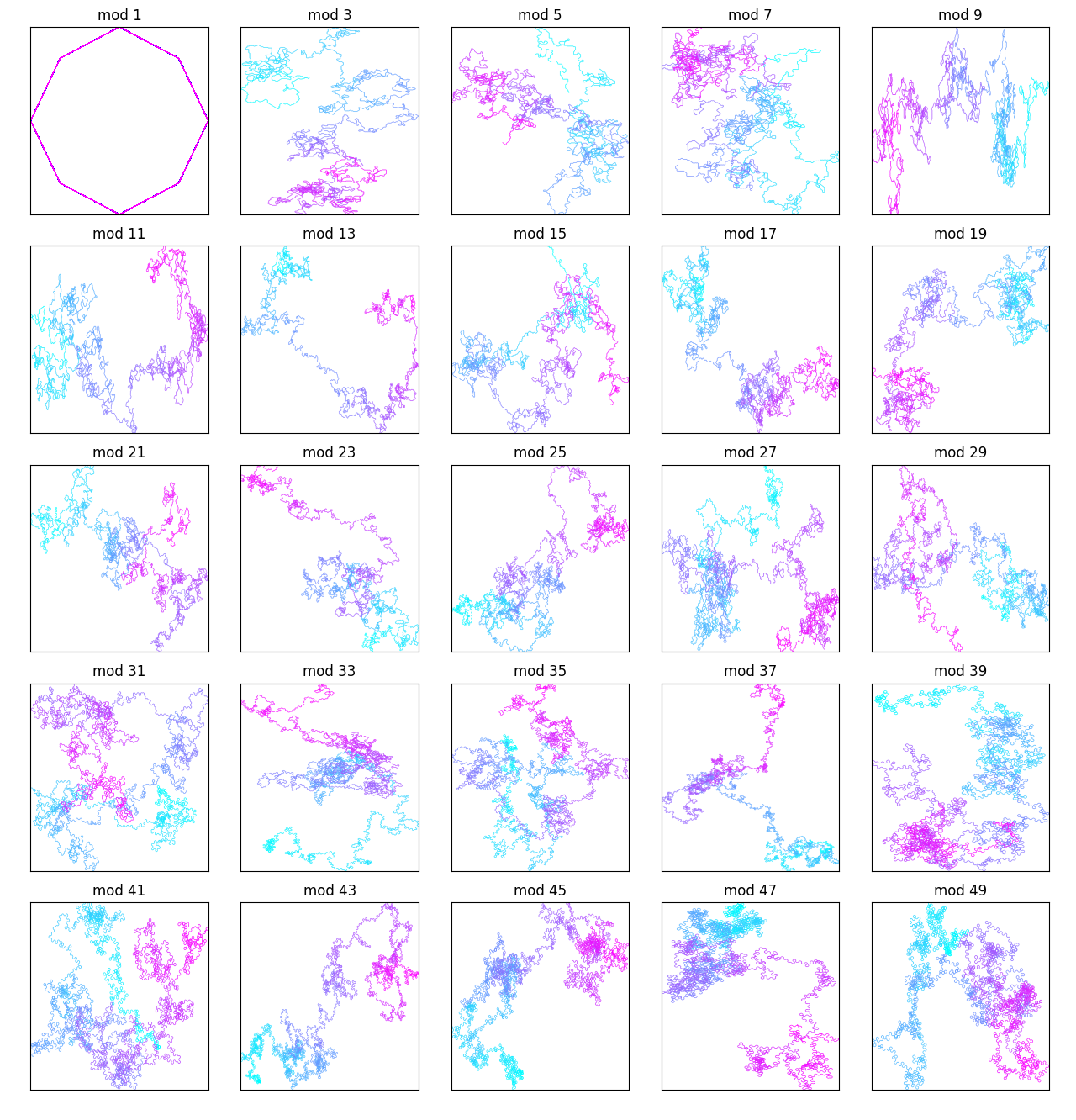
The prime numbers are another fun sequence of numbers:

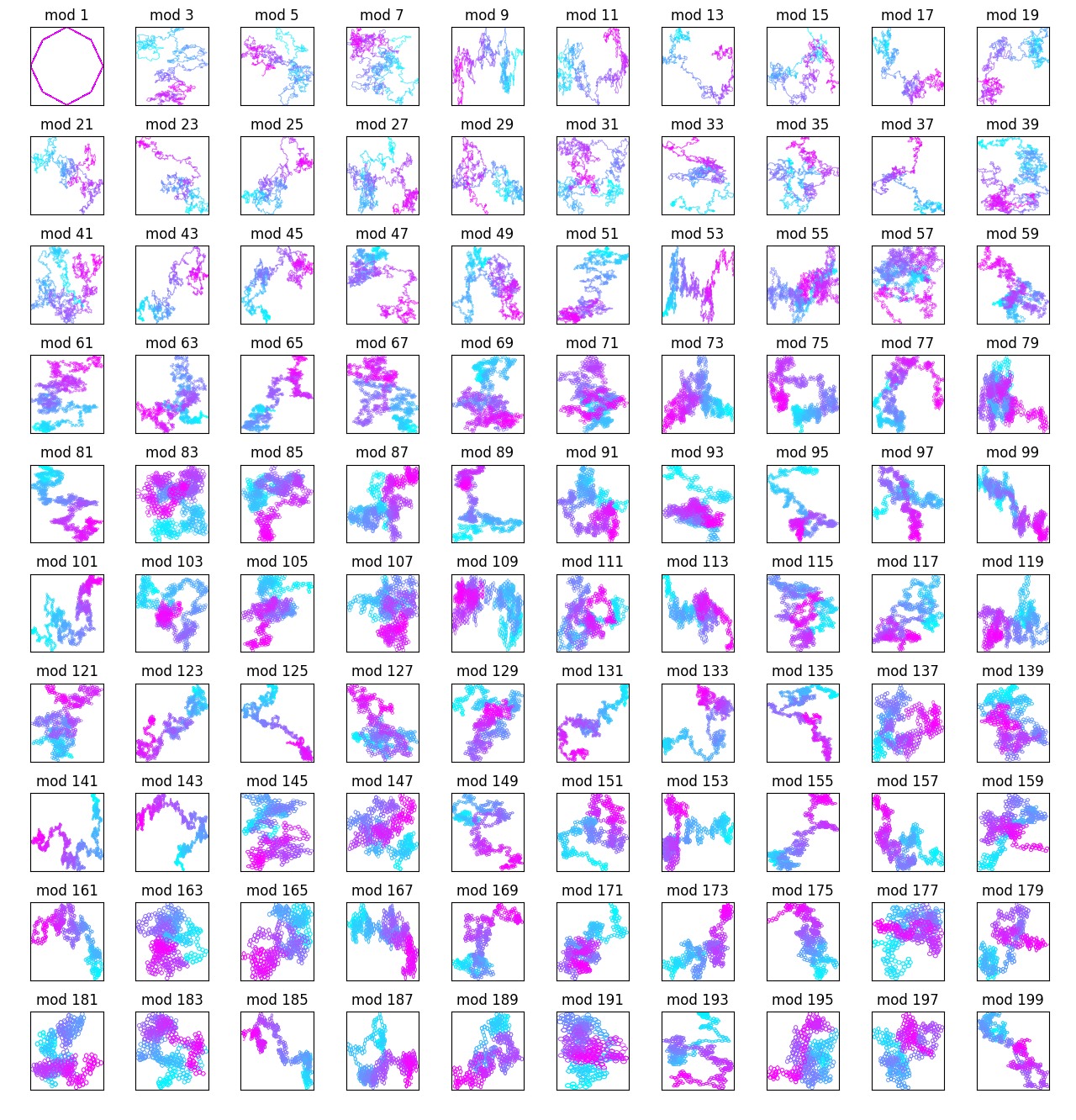
At first, it looks like they're just random walks. But upon further inspection, there are some patterns here.

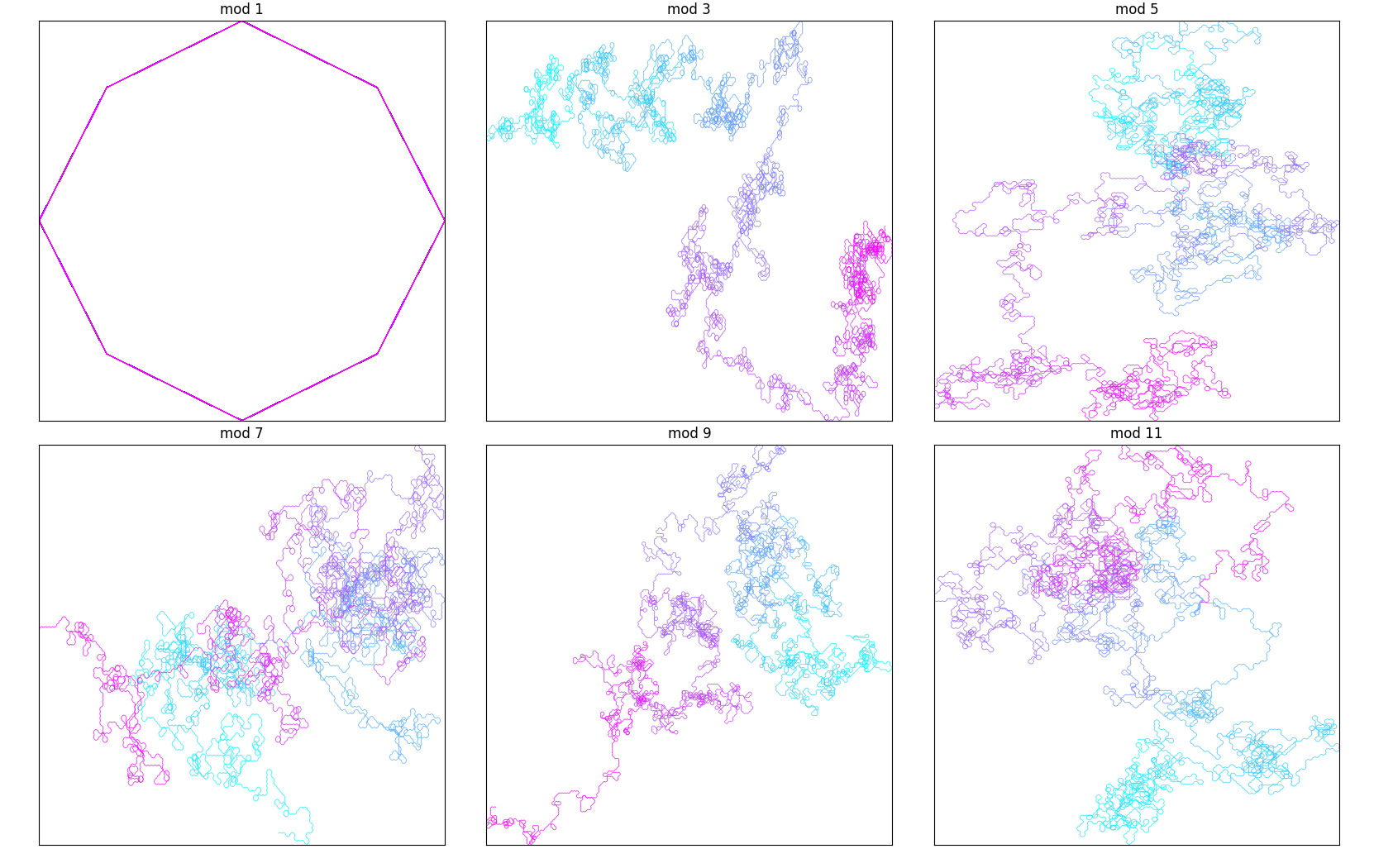
For the first 50 mod constants, you can't really see much:

But as you get into higher mod constants, that changes:

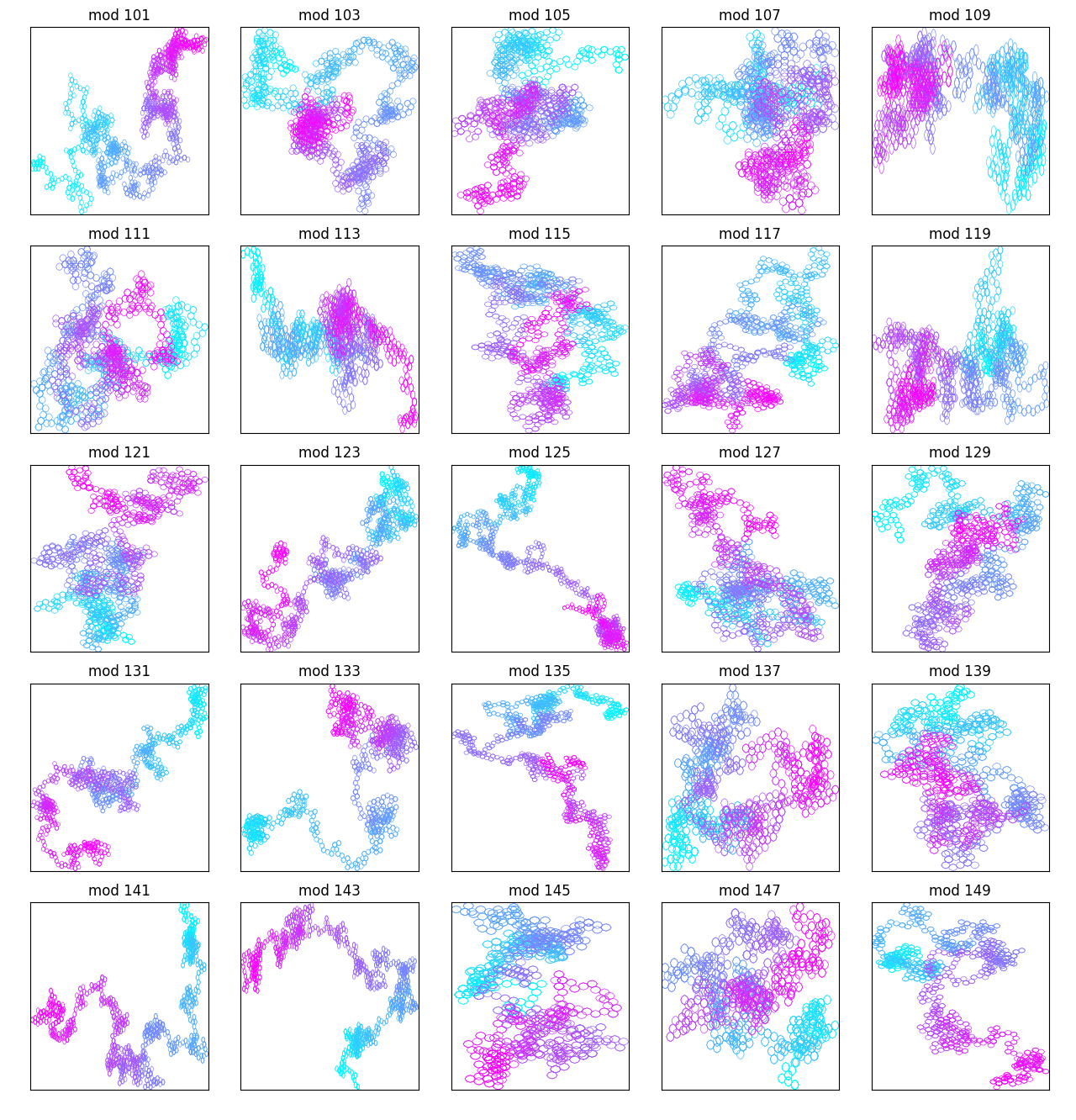
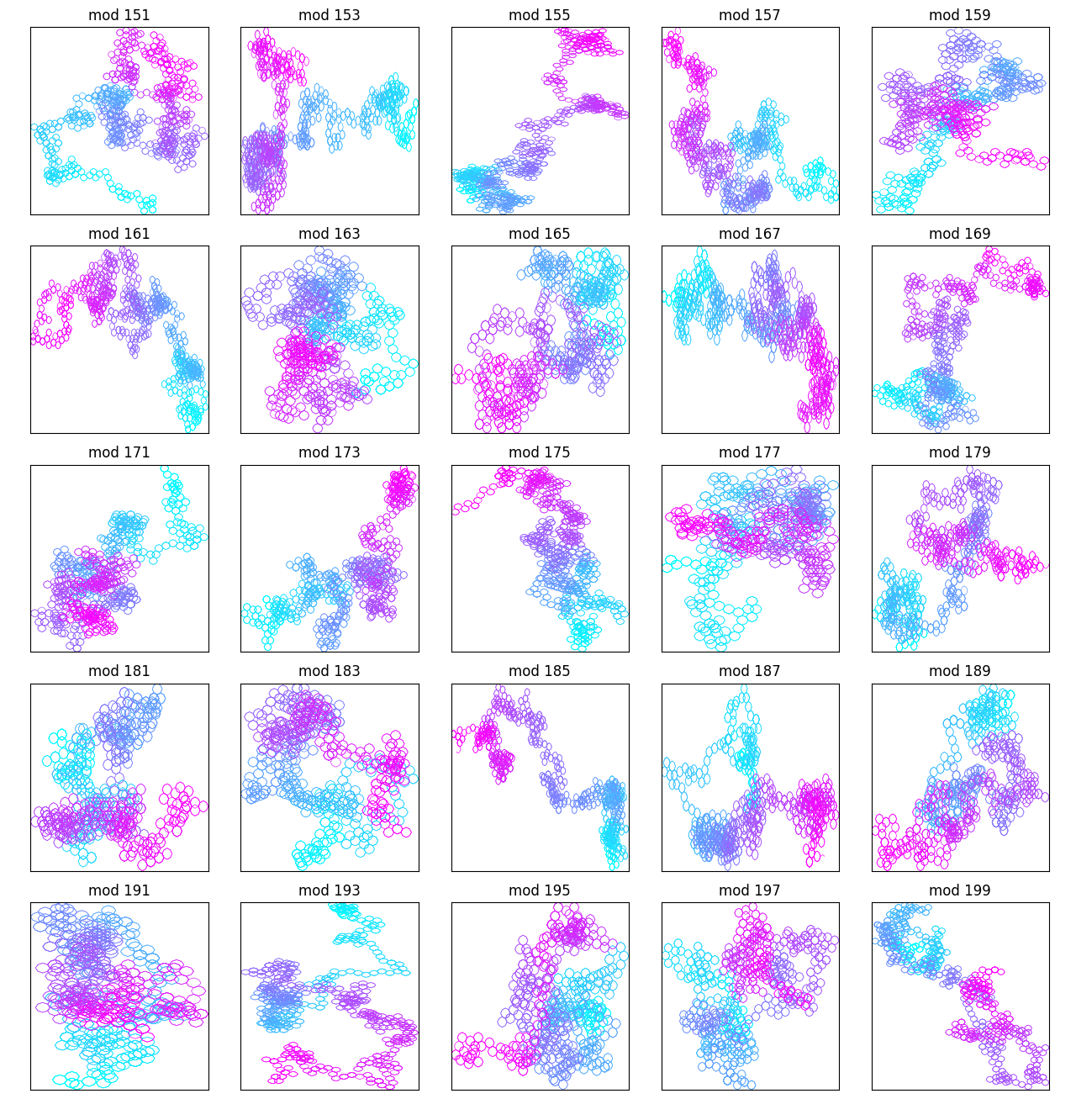
Pretty cool.

And here are the primes from 1 to 100 including evens:

This is also interesting.

Digits of pi

The next sequence I looked at were the digits of pi, which seemed really interesting until I remembered that they're stuck in the range $[0,9]$:

Zooming in on the first 6 odd mod constants doesn't reveal anything earth-shattering:

Palindromes

I was running out of sequences that I knew how to check easily so I tried looking at palindromes. These actually produced some pretty interesting results:

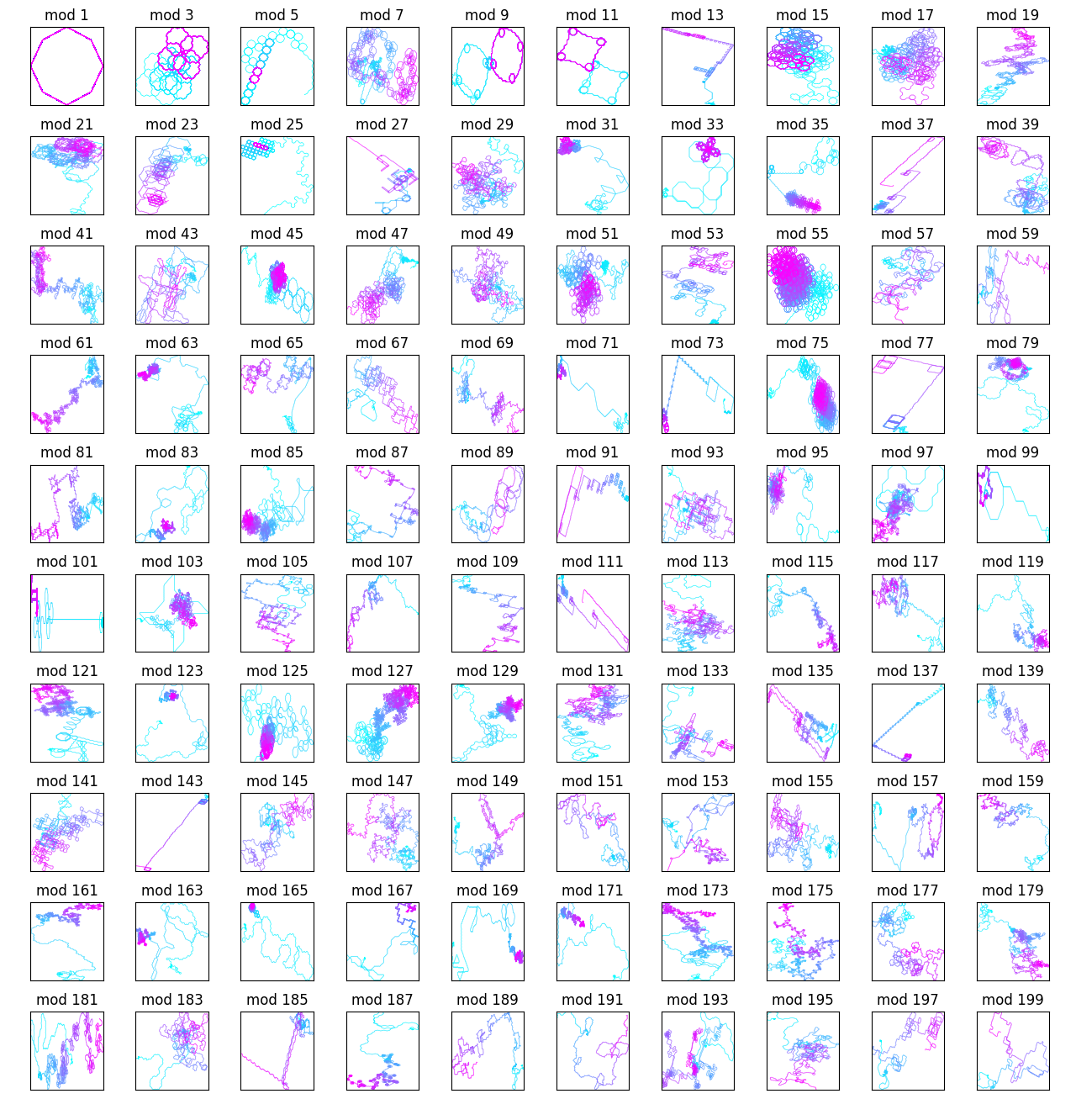
...although most of the interesting ones seemed to have mod constant less than 50:

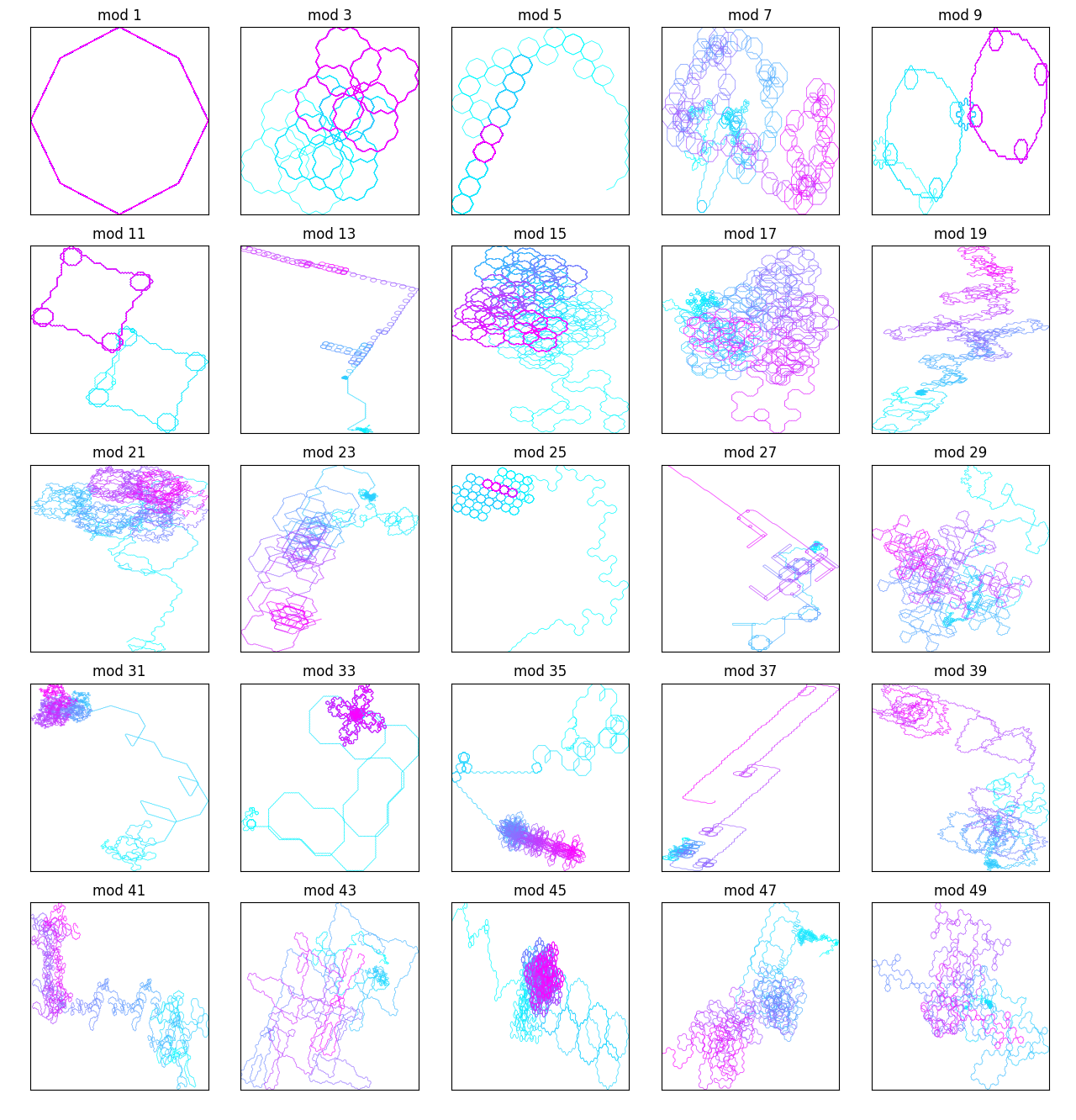
After this I looked at binary palindromes (numbers that had palindromic binary representations):

...and the ones with mod constant below 50:

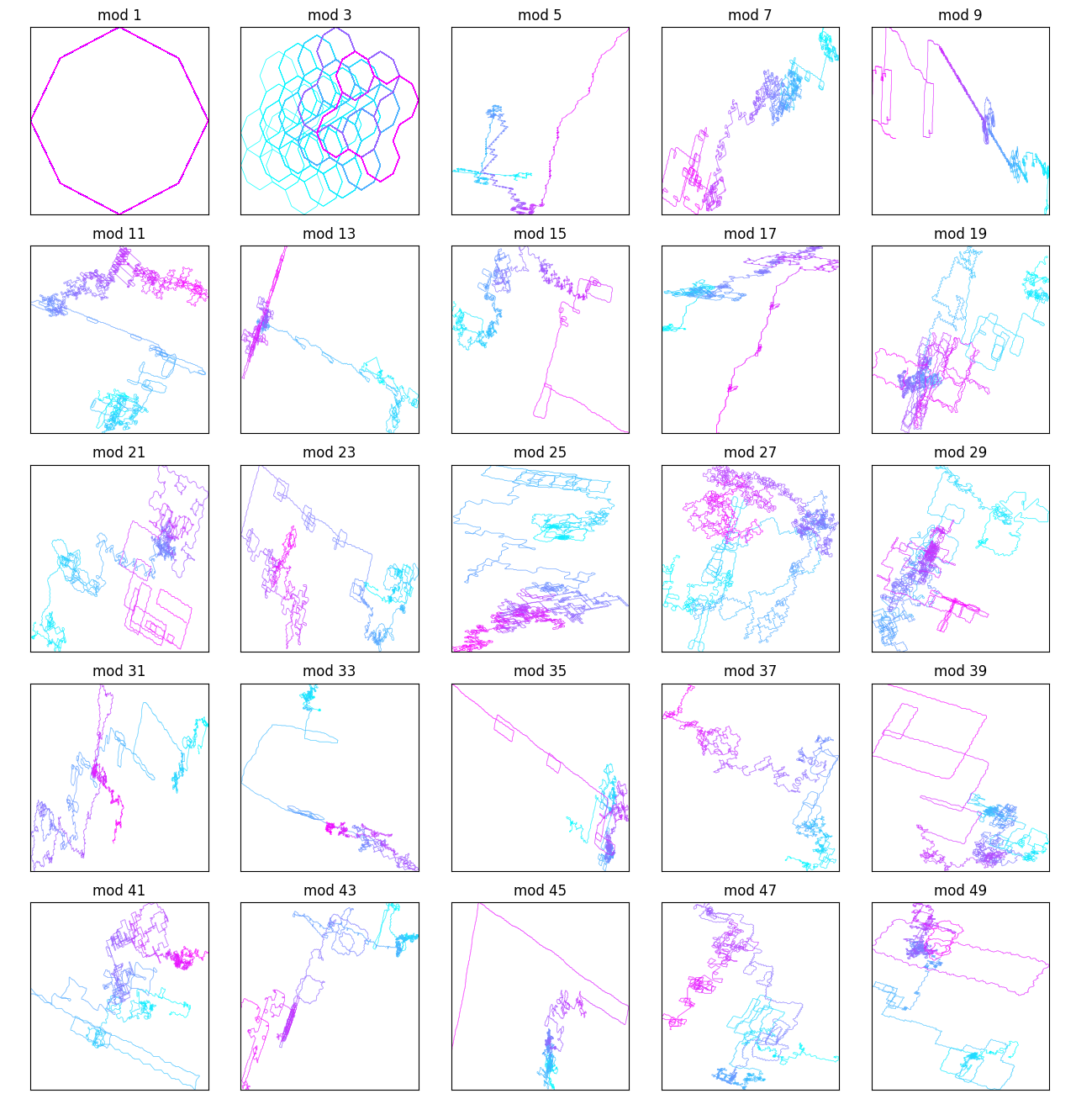
I thought the mod constant of 3 looked the coolest for the binary palindromes:

Conclusion

And that's all the sequences I looked at. Definitely some cool stuff!

You can find the code here: GitHub gist. It's kind of messy.