The Volume of an Open-Top Cone

Ben Rosenberg

Say we have an open-top cone, such as the one seen below:

Getty Images, via NYPost

Say we’re given the height of this cone, its bottom radius (the radius of the circle of its base), and the top radius (the radius of the smaller circle at the top).

Let the height of the open-top cone be h, its bottom radius be R, and its top radius be r. It’s obvious that we can find the volume of the open-top cone by following these steps:

In order to find the volume of the corresponding closed-top cone, we need to first find the height of the closed-top cone. Let’s call this height H.

Note that H is the rightmost side of the set of similar triangles in the figure below.

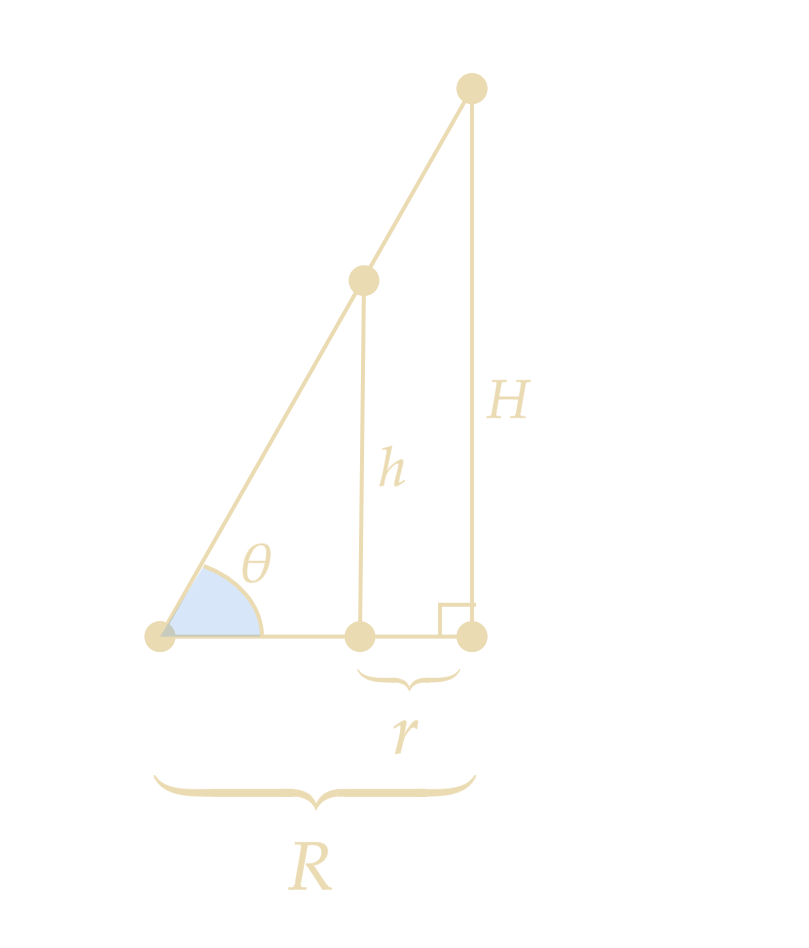
Figure 1: Similar triangles (image made with Matcha.io)

Since the smaller and larger triangles are similar triangles, their sides are related by some ratio. The ratio in this case is R-r : R. So, if we multiply the smaller height by \frac{R}{R-r}, we will get the larger height: H = \frac{Rh}{R-r}

Now that we have our closed-top height, we can find the volume of the closed-top cone.

Recalling the formula for the volume of a cone, we get V_\text{closed-top} = \frac{1}{3} \pi R^2 H. Plugging in our value for H gives V_\text{closed-top} = \frac{1}{3} \pi R^2 \frac{Rh}{R-r} = \frac{\pi R^3 h}{3(R-r)}.

Now that we have the volume of the closed-top cone, let’s find the volume of the “removed” cone – the “missing” top of our open-top cone. This is another simple application of the formula for the volume of a cone: V_\text{removed} = \frac{1}{3} \pi r^2 (H-h) = \frac{1}{3} \pi r^2 \left(\frac{Rh}{R-r}-h\right)

We can now subtract the removed volume from the closed-top volume to obtain the volume of the open-top cone: \begin{aligned} V_{\text{open-top}} &= V_\text{closed-top} - V_\text{removed} \\ &= \frac{\pi R^3 h}{3(R-r)} - \frac{1}{3} \pi r^2 \left(\frac{Rh}{R-r}-h\right) \\ &= \frac{\pi h}{3}\left[\frac{R^3}{R-r} - r^2 \left( \frac{R}{R-r} - 1 \right)\right] \\ &= \frac{\pi h}{3}\left[\frac{R^3}{R-r} - r^2 \frac{R - (R-r)}{R-r}\right] \\ &= \frac{\pi h}{3}\cdot\frac{R^3 - r^3}{R-r} \end{aligned}

We could leave our answer like this, or simplify further using the formula for the difference of two perfect cubes: x^3 - y^3 = (x-y)(x^2 + xy + y^2)

\begin{aligned} V_{\text{open-top}} &= \frac{\pi h}{3}\cdot\frac{R^3 - r^3}{R-r} \\ &= \frac{\pi h}{3}\cdot\frac{(R-r)(R^2+Rr+r^2))}{R-r} \\ &= \frac{\pi h}{3}\cdot (R^2 + Rr + r^2) \end{aligned}

This isn’t that much more simplified though.